Fighting Bots with the Client-Puzzle Protocol

In 1999, Ari Juels and John Brainard came up with an elegant protection against denial of service attacks, known as the client-puzzle protocol. Their idea was patented (US patent 7197639), which might have inhibited its uptake. However that patent expired in early 2020, so it is now free for anybody to use. And it should be used.

The client-puzzle protocol is not widely known or implemented, but we do note that Akamai picked up the concept very soon after the patent expired for their bot manager. Akamai adds advanced intelligence to it (remark: it appears that Clouflare may be doing the same, see also Kasada), but the basic client-puzzle protocol is easy to implement and can be used by anybody without spending a dime.

This blog:

• Explains the basic idea (slightly simplified) behind the Juels-Brainard client-puzzle protocol with the focus on web applications,
• Links to proof-of-concept source code,
• Links to a demo of the source code hosted on Heroku,
• Explains why it is preferable over rate limiting when protecting against malicious bots,
• Suggests implementation enhancements to get the most benefit of it,
• Provides references to related work.

Client-Puzzle Protocol

The objective in the client-puzzle protocol is to slow down bots so that they become near the speed of humans. Slowing them down impedes a number of different attacks, such as web scraping, brute forcing, and certain types of denial-of-service.

To accomplish this, the proof-of-work concept is used. Now many people may be thinking about Bitcoin, but the proof-of-work concept existed in cryptographic literature more than a decade before Bitcoin was invented. In fact, Ari Juels was one of the pioneers of the concept.

The client-puzzle protocol serves a cryptographic puzzle to clients that must be solved before their request is served. The puzzle may take a fraction of a second to solve — which has little impact on legitimate humans, but slows down bots significantly. The verification of the puzzle solution is very fast, so the protocol imposes negligible impact on the server. Also, the protocol is entirely stateless.

To be concrete, the puzzle typically involves finding part of the pre-image of a cryptographic hash function. See the diagram below.

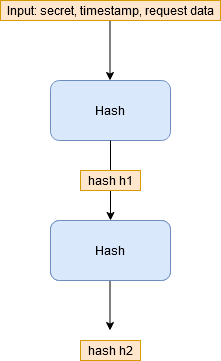
In this construct, two levels of hashing are used. First, the client request data (query parameters/request body) along with a server-side secret and timestamp are hashed. This produces hash h1, which is hashed to produce hash h2. The puzzle consists of h2 and most of the bits of h1.

Cryptographic hash functions are designed to be pre-image resistant, so if you are given h2, then it would be very difficult/time consuming to find h1. On the other hand, if you are given h2 along with most of the bits of h1, then you could brute force the remaining bits provided that the number of remaining bits is not too large. You would simply try each possibility for the remaining bits, hash the candidate pre-image, and see if the hash matches h2. If k bits are missing, then this requires up to 2^k trials. It is easily done for small k, but requires some computational effort.

In the client-puzzle protocol, h2 and most of the bits of h1 are given to the client. The client must brute force the remaining bits. When the client succeeds, it sends back the puzzle solution (h1), the timestamp that the server provided, and the request data.

Now consider how the server verifies the result. This is the most elegant part because the server does not need to remember h2. Instead, it just recomputes h1 by hashing its secret along with the client provided request data and timestamp. If the hash matches what the client provided, then the puzzle is solved!

Clients cannot forge fake puzzles as long as they do not know the server secret. Attempts at providing fake puzzles are easily caught and rejected from the computation just described. This computation is quick and easy to do for the server: a single hash computation with no database usage. Similarly, clients cannot lie about the timestamp because the hash computation will not check out.

What’s the purpose of the timestamp? You can set an expiry time by which the puzzle must be solved. This gives the option of denying the request if the solution took too long, which is especially useful if the response for the request may change over time. For example, consider prices of items on an ecommerce website. Without the timestamp, the attacker can provide the same puzzle solution every week without recomputing it to get weekly price updates. With the timestamp, it forces him to recompute every time.

Generally, the use of this protocol would look like this for a web application:

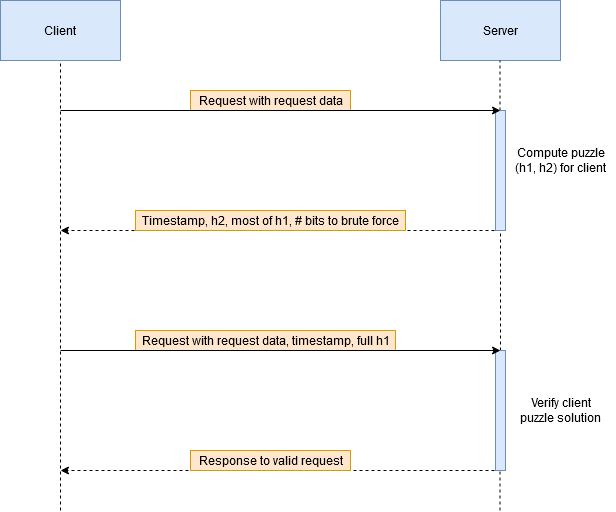
When Juels and Brainard wrote about this protocol in 1999, they described protecting against threats such as TCP SYN flooding, email bombs, and so on. The internet has flourished since then, and today it is more clear that there are many applications of this technology not only for preventing denial of service attacks, but more generally for impeding bot activity such as the way Akamai is using it.

Source Code and Demo

I am not a professional programmer and I am just learning Node.js, but despite that it was little effort for me to build a proof of concept. You can see the source code on GitHub. This PoC takes user input for a search query and returns a random gif from Giphy related to the search query. The server side uses a Giphy API key. By using client-puzzle protocol, clients need to do a computation every time a request is made through the server to Giphy, which controls the number of requests going to Giphy through the server.

The main functions on the server side are compute_puzzle( ), which computes the puzzle from the original request, and check_puzzle_solution( ), which verifies the solution. The client side has code to brute force the puzzle solution.

You can see the demo here. The puzzle strength is set at 2¹⁷ and the expiry time is 10 seconds. This usually takes less than a second on most of my devices, with exception to my old iPad 2, where it can take a few seconds. Note that every request is using my Giphy development API key, which is rate limited by Giphy. Although I do not know what the rate limit settings are, I’m counting on the client-puzzle protocol to (hopefully) keep my anonymously accessible demo application below the bar.

If you’re going to use my GitHub code, here are a few remarks you should be aware of:

• The code generates the secret from crypto.randomBytes( ) upon startup, which is fine if you have only a single backend server. If you’re using multiple servers, the secret should be shared among them to deal with the case that the server that responds to the puzzle solution might not be the same as the server that created the puzzle.
• The whole security of the system depends upon the strength of the secret, so don’t use something silly like P@55w0rd123. The secret needs to be long and not brute-forceable.
• The program is most entertaining with a Giphy API key that you can obtain quickly and for free following guidance here. Once you have the key, set it as the environmental variable giphy_api_key.
• You can also set the puzzle strength (environmental variable puzzle_strength, 16 by default which means 2¹⁶ effort) and expiry time (environmental variable time_limit, 5000 milliseconds by default).
• Ultimately the client-side JavaScript code should be optimised. This is because the JavaScript code is what legitimate users will be using whereas a good hacker would use custom code to solve the puzzle as fast as possible. The more he can make his code faster than the JavaScript code, the more beneficial it is to him (more details in last section below). To optimise the legitimate client code, the focus should be on making sha256 as fast as possible.

The limits of rate limiting

Rate limiting is very important, but there are certain attack scenarios where rate limiting does not provide sufficient protection.

If you have an API that is accessible anonymously, the typical approach for rate limiting is to limit by IP address. However, nowadays hackers easily get around that restriction by rotating their IP address using tools such as Fireprox. Hackers can also spoof geographical locations, and easily blend in to look like legitimate users. As a consequence, it is hard to distinguish between the bad guy versus legitimate users — you either let the bad guy requests in for free or you take the risk of dropping legitimate user requests.

When battling malicious clients that are accessing anonymously accessible content, rate limiting is most effective if a decision can be made with certainty on whether the client is malicious. This certainty will not exist against a clever adversary.

The client-puzzle protocol handles the uncertainty much better by requiring every client to solve a puzzle. Legitimate users (people) do not make numerous requests per second, so they will see little impact. Malicious bots on the other hand will see a huge impact because they are forced to do computations for each of their numerous requests, and that builds up. With the client-puzzle protocol, making requests is no longer free.

Of course, there could be legitimate bots where there is a need to do many requests per seconds. Those can be identified in any number of ways (API key, known IP address, etc…) and whitelisted to allow them through. Everybody else must do the computation per request.

Implementation enhancements

Before talking about enhancements, we must talk about limits. The client-puzzle protocol does not stop bots, it only slows them down. A malicious entity can still get requests through, but suddenly it has to “pay” per request, where the payment is by computation time. If the entity has substantial computing power, it can erase much of the benefit that the protocol offers.

In the original publication, Juels and Brainard suggested only using the protocol when the server is under attack and tuning the parameters according to the severity of attack. They also had in mind attacks such as TCP SYN flooding, where a server can only handle so many connections at once. Our focus is more at the application layer, so we will discuss application-specific enhancements. Of course tuning parameters according to severity is still a valid protection.

The following implementation enhancements can also be considered:

• Similar to Akamai/Cloudflare/Kasada, we might have some intelligence about our adversary, allowing us to adjust the puzzle strength according to the likelihood of the request being malicious. For example, maybe we know that the attacker is using a particular API key or user agent header — we can offer tougher puzzles to those requests than for other requests.
• If we are trying to defend from an attacker brute forcing specific targets, then we can cache failed efforts and increase puzzle strength for those specific targets upon each failure. These increases in strength should be temporary: long enough to frustrate the enemy, not too long to lock out the good guys.
• We can always whitelist known good clients to allow them through with little effort, while requiring higher puzzle strength for the unknown.

Remark: Although it will reduce impact, the client-puzzle protocol is not by itself strong enough to prevent credential stuffing attacks because the attacker has a significant probability of success per request. For a more appropriate defence, see our OT2FA blog. The client-puzzle protocol does help impede other forms of brute force where the likelihood of success per request is smaller.

Related work

One of the shortcomings of the client puzzle protocol is that the attacker might have significant more computational resources than legitimate users. This is known as the resource disparity problem. Guided Tour Puzzle Protocols were designed to address this disparity. I have not yet researched their practicality or intellectual property considerations.

In private communication, Ari Juels suggested that client puzzles could potentially be used for mining a cryptocurrency such as Monero (having an ASIC-resistant proof-of-work scheme), “meaning that users are effectively paying for services.” After some number crunching, he said it would unfortunately not yield much currency because the clients on the whole aren’t doing a huge amount of work. Ari also pointed out how this was discussed in a related paper from 1999 with Markus Jakobsson where they applied the idea to a cryptocurrency protocol known as MicroMint.